Nuclear Magnetic Resonance (NMR) Spectra
Background
On their own, computed shielding values and J-couplings from static molecular structures can be used to interpret experimental NMR spectra, but directly plotting calculated shielding and J-coupling values will usually result in poor agreement with experiment. For rigid molecules in which all 1H atoms are equivalent, such as tetramethylsilane (TMS), calculated shielding values from a single point calculation may serve as a reference that is comparable to experiment. However, molecular motion, solvent environments, hydrogen exchange processes and other phenomena mean that the shape of NMR spectra is rarely a direct mapping of calculated shieldings and J-couplings. For example, the interaction timeframe of a radio frequency pulse with a nuclear spin is of the order of a microsecond, much longer than timescales associated with nuclear motion and certain exchanges. We exemplify the process of interpreting an experimentally obtained 1H NMR spectrum of ethanol, using experimental data obtained from ChemicalBooK. First, the experimental spectrum of ethanol itself is far from unique, but instead depends heavily on factors such as solvent used and concentration. Among the five very different spectra included in ChemicalBooK book at the time of writing, we focus on a spectrum obtained for 0.04 ml ethanol in 0.5 ml CDCl3 obtained at 89.56 MHz. The spectrum exhibits a set of well defined peaks, schematically redrawn in Figure 1(a). In this instance, the spectrum shows clearly resolved groups of peaks that may be attributable to the CH2 group (red), CH3 group (green) and OH group (blue). The CH2 and CH3 peaks show splittings that can be attributed to interaction between both groups via J-couplings. This tutorial will provide a brief guide to producing an NMR spectrum and iterative improvements to refine this spectrum.
Tutorial
In this tutorial, we will systematically recreate the NMR spectrum of ethanol (CH3CH2OH).
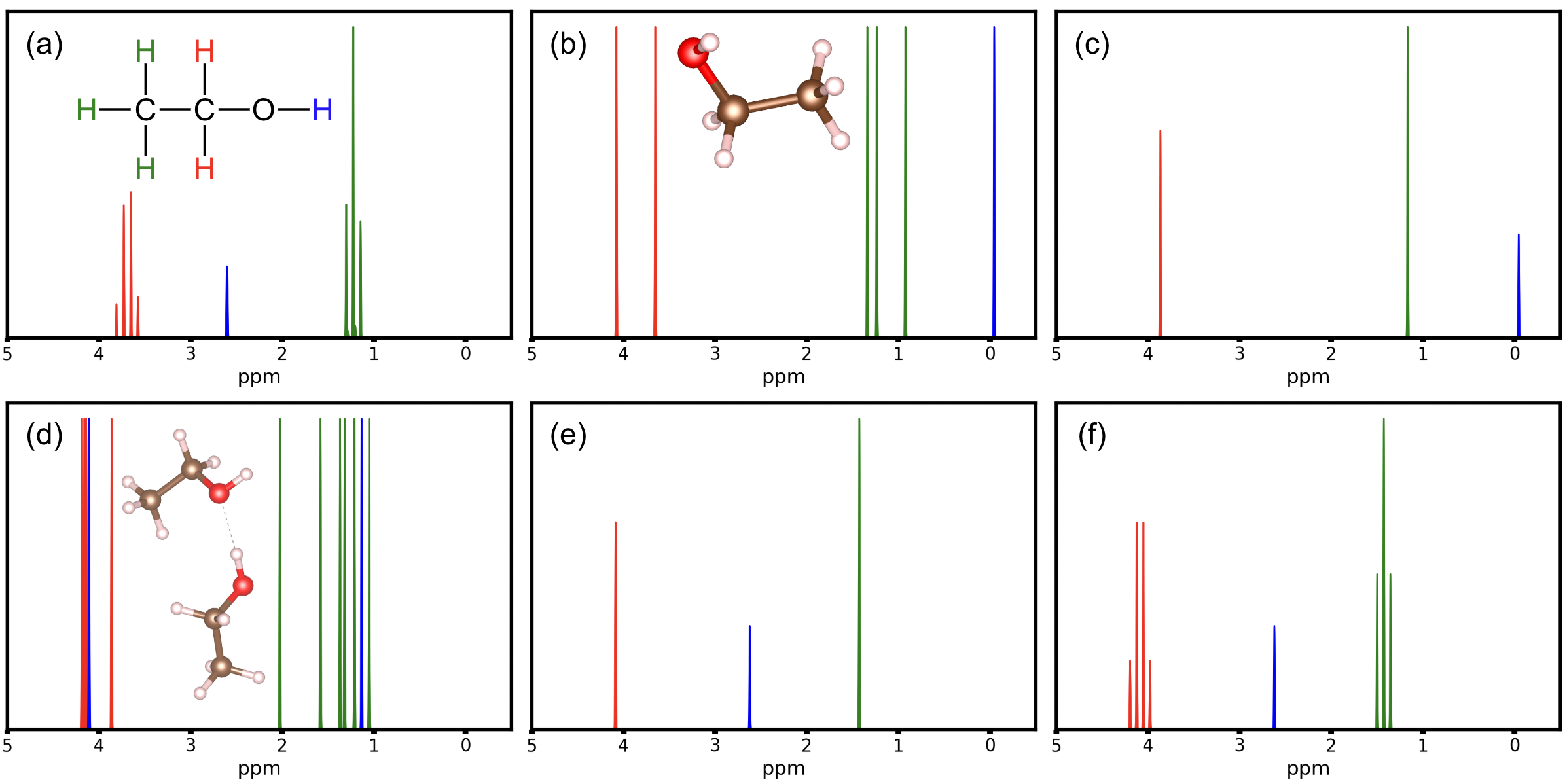
Figure 1: (a) Peaks in the experimental Ethanol \(^1\)H NMR spectrum at 89.56~MHz for 0.04 ml ethanol in 0.5 ml CDCl3, schematically redrawn from (Data from Chemical BooK). Red, blue, and green peaks are tentatively attributed to signals from the CH2 group, OH group, and CH3 group, respectively. (b) DFT-PBE single point calculation of 1H chemical shifts with respect to TMS, for a single ethanol molecule (inset). (c) Same data as (b) with signals averaged across the CH2 and CH3 groups in ethanol. (d) Data pertaining to a DFT simulation of the molecular dynamics (see text for details) of a hydrogen-bonded ethanol dimer (inset). Structures were sampled from this ensemble and the NMR response for each atom was averaged across these samples and visualized. (e) Same data as (d) with signals averaged across each of CH2, CH3 and OH. (f) Same data as (e) but including the peak splitting due to J-coupling between H atoms in the CH2 and CH3 groups. This figure is set to be published in an upcoming FHIaims Roadmap.
Step 1: Geometry Preparation
First, the experimental geometry of ethanol was found on PubChem and translated to the geometry.in file format for FHIaims as follows:
atom -1.1712 0.2997 0.0000 O
atom -0.0463 -0.5665 0.0000 C
atom 1.2175 0.2668 0.0000 C
atom -0.0958 -1.2120 0.8819 H
atom -0.0952 -1.1938 -0.8946 H
atom 2.1050 -0.3720 -0.0177 H
atom 1.2426 0.9307 -0.8704 H
atom 1.2616 0.9052 0.8886 H
atom -1.1291 0.8364 0.8099 H
Figure 2: Input Ethanol Geometry (as visualized with JMOL)
In the present simulation, this structure was optimized (i.e., its total energy was minimized) using the following control.in file:
xc pbe
vdw_correction_hirshfeld
relativistic atomic_zora scalar
relax_geometry bfgs 5e-3
spin none
+ ['tight' FHIaims species defaults for H, C, and O]
This calculation should converge quickly (23 seconds locally on my MacBook with an M1 processor). The relevant portion of the resultant geometry.in.next_step file was computed as:
atom -1.22782808 0.27220854 -0.00620805 O
atom -0.04782759 -0.53900672 0.01791495 C
atom 1.24070776 0.27281531 0.00036829 C
atom -0.06164303 -1.21911023 0.88941819 H
atom -0.11806789 -1.16608127 -0.88155034 H
atom 2.11685863 -0.39088742 -0.03356413 H
atom 1.27268434 0.93427021 -0.87530125 H
atom 1.33264898 0.89452226 0.90371533 H
atom -1.21843310 0.83576931 0.78290700 H
Step 2: Single-point NMR Calculations
With an optimized geometry, 1H shielding values can now be computed. See the Shieldings tutorial for a further explanation. The input geometry.in and control.in files read as follows:
atom -1.22782808 0.27220854 -0.00620805 O
atom -0.04782759 -0.53900672 0.01791495 C
atom 1.24070776 0.27281531 0.00036829 C
atom -0.06164303 -1.21911023 0.88941819 H
magnetic_response
atom -0.11806789 -1.16608127 -0.88155034 H
magnetic_response
atom 2.11685863 -0.39088742 -0.03356413 H
magnetic_response
atom 1.27268434 0.93427021 -0.87530125 H
magnetic_response
atom 1.33264898 0.89452226 0.90371533 H
magnetic_response
atom -1.21843310 0.83576931 0.78290700 H
magnetic_response
xc pbe
vdw_correction_hirshfeld
spin none
relativistic atomic_zora scalar
basis_threshold 0.0
magnetic_response s
+ ['NAO-VCC-5Z' FHIaims species defaults for H and 'tight' species defaults for C and O]
Note the more expensive NAO-VCC-5Z species defaults are only used for the hydrogen atoms which saves computational cost without harming performance. In experimental NMR, results in ppm are recorded as shifts with relation to a standard sample. In this case, the ethanol spectra was calibrated from a baseline of tetramethylsilane (TMS). In TMS, the computed 1H shielding with FHI-aims is ~31.03126 ppm so all results are computed as shifts from this value. From this computation, shielding values can be found in the human-readable aims.out standard output. In Table 1, computed total isotropic shieldings and TMS-shifted readings can be found. Throughout the rest of this tutorial all results will be shifted by this TMS baseline.
| Atom # | Computed Shielding | Chemical Shift |
|---|---|---|
| 4 | 27.10640 ppm | -3.92486 ppm |
| 5 | 27.53035 ppm | -3.50091 ppm |
| 6 | 29.94804 ppm | -1.08322 ppm |
| 7 | 29.84444 ppm | -1.18682 ppm |
| 8 | 30.26037 ppm | -0.77089 ppm |
| 9 | 31.22923 ppm | 0.19797 ppm |
The general convention when plotting NMR spectra is to invert both the sign of the chemical shift and also the x-axis (values increase left to right) as can be seen throughout Figure 1. Figure 1(b) plots these computed results for a single-point NMR spectra. In comparison to Figure 1(a), although no J-couplings are yet considered in the computed spectrum, there is more than one peak per CH2 and CH3 group, respectively, and the peak associated with the OH group is far off. One obvious measure to achieve physically more appropriate results is to account for averages between the H atoms within the CH2 and CH3 groups, respectively, leading to the spectrum shown in Figure 1(c). In this figure, the peak intensity is scaled to the number of atoms represented by a given peak. The CH2 and CH3 peaks are now reassuringly close to the related peaks in the experimental spectrum, though still without accounting for J-couplings. However, the peak associated with OH is far off. Similar observations can be made for 1H ethanol spectra in different solvents in which the CH2 and CH3 peaks remain roughly in the same locations but the position of the OH peak varies widely. Typically, the OH peak is expected to be impacted by hydrogen bonding and H exchange, depending on the solvent environment.
For some highly symmetric molecules, such single point calculation spectra may be sufficient to explain experimental results, however for most systems, continuing to step 3 and beyond may be necessary to recreate the experimental peaks.
Step 3: Time- and Symmetry-averaged NMR Calculations
For the specific conditions in Figure 1(a), a better interpretation of the experimental spectrum can be arrived at by testing specific hypotheses for the ethanol coordination and environment in direct computations. First, each ethanol molecule undergoes molecular motion; second even in dilute conditions, aggregation of two or more ethanol molecules to form hydrogen bonds could occur. The minimal geometry input which has a possibility of probing such aggregation is an ethanol dimer.
In order to test this hypothesis, we start by creating a geometry.in file with two ethanol molecules H-bound together. Using analogous settings to Step 1, this geometry was then optimized leading to the following geometry.in which will be used as an input to the NMR calculations:
# ethanol 1
atom 2.77209484 1.27496144 0.76590318 C
atom 2.05271538 2.14693788 1.77484692 C
atom 3.01275872 2.57700175 2.76531480 O
atom 2.06108696 0.89836842 0.01875799 H
atom 3.23985953 0.41360050 1.26045289 H
atom 3.55108458 1.84453733 0.24281152 H
atom 1.60663840 3.02439164 1.27681394 H
atom 1.24238263 1.58417252 2.26837102 H
atom 2.56316695 3.15838112 3.39729254 H
# ethanol 2
atom 7.47674108 3.45043398 0.68520271 C
atom 6.34954958 2.90110763 1.54092291 C
atom 5.25062008 3.80799938 1.48483984 O
atom 8.34599264 2.77881761 0.70831770 H
atom 7.79210166 4.43718973 1.05000286 H
atom 7.15217799 3.56189852 -0.35821422 H
atom 6.05042616 1.90017754 1.17396081 H
atom 6.69688771 2.77061256 2.58378972 H
atom 4.50851512 3.41301047 1.98821288 H
From this optimized geometry (see the inset of Figure 1d) we can see the hydroxyl group of one ethanol is involved in H-bonding while the hydroxyl group of the other ethanol, similar to the single ethanol case, is not. The most straightforward way to account for molecular motions at finite temperature is an ab initio molecular dynamics simulation. Depending on the system studied, many different choices can be made, but for this system, the following control.in file is sufficient:
xc pbe
vdw_correction_hirshfeld
relativistic atomic_zora scalar
MD_run 10.0 NVT_parrinello 300 0.5
MD_time_step 0.001
MD_MB_init 300
MD_restart .true.
output_level MD_light
+ ['tight' FHIaims species defaults for H, C, and O]
Particularly, this runs a NVT molecular dynamics ensemble using the stochastic velocity rescaling thermostat of Bussi, Donadio and Parrinello (BDP), set to 300K over 10ps with 1.0 fs steps. The characteristic collision time of the thermostat is set to 0.5 ps - not long, but hopefully long enough to not impact the overall dynamics unduly compared to the physical system. ("Thermostats" do not exist in experiment. In computational simulations, they are added as artificial terms to Newton's equations but they must not strongly impact the dynamics to yield physically reasonable results. For the BDP thermostat, a longer collision time will lead to results that are closer to physically correct dynamics, but at the price of a longer initial equilibration period that does not yet reflect the thermalized atomic motions.)
Due to the small size of ethanol, the use of tight species defaults is possible here. In many cases for similar time scales, intermediate or light species defaults will provide sufficient accuracy while allowing a long enough overall trajectory to properly average over the molecular motion. Despite the small size of ethanol, this "tight" molecular dynamics calculations still may take a relatively long time (~1 day run on a single, quite old (2014) compute node with 20 cpu cores). The FHI-aims code distribution comes prepackaged with a utility to retrieve all geometry.in files from a molecular dynamics run. Assuming the FHI-aims directory is labelled as $AIMS and the MD directory is the current directory, run the following on the command line:
$AIMS/utilities/create_geometry_zip.pl ./aims.out
This will extract all geometries from the output file aims.out and store them in the compressed geometries.zip directory. Programs like JMOL are able to visualize the structures visited during this molecular dynamics run. As a first approximation, this tutorial will assume we simply want an average of all molecular motions without any specific motion needing to be perfectly described. For cases where this approximation is insufficient, see the Further refinements section for guidance on picking geometries to average the results from.
Given the collision time of 0.5 ps set for the BDP thermostat, the first ~1ps of a molecular dynamics simulation was not used as the geometry is "equilibriating" to temperature from the energy-minimized single-point geometry and might not reflect the physical dynamics of an equlibrated molecule. In order to approximately capture all motions, 10 structures were uniformly sampled from the remaining 9ps of the molecular dynamics simulation. For each structure, the 1H shieldings were computed as described above. By averaging over shifts for each H atom individually, distinct "time-averaged" peaks for each of the 12 hydrogen molecules in the ethanol dimer were computed and plotted in Figure 1(d). Note that the signal from hydrogen-bonded OH group (blue, ∼4 ppm) is drastically shifted compared to the non-hydrogen bonded OH (blue, ∼1 ppm). Beyond this, the CH2 and CH3 peaks appear approximately in the correct location but the multiplicity of peaks is aphysical.
Further averaging over chemical 1H associated with CH3, CH2 and OH groups in both molecules, respectively, leads to the spectrum shown in Figure 1(e), with peak locations in good agreement with Figure 1(a). This averaging can be rationalized by considering the molecular motions, hydrogen exchange, and continuous association and dissociation which would be observed in much larger samples of ethanol molecules at time frames longer than may be probed through ab inito molecular dynamics. The cumulative effect of these factors is each hydrogen within a "symmetry group" such as a CH3 group experiences some combination of all possible configurations and thus the experimental response is measured as an "average" of the distinct possible peak locations simulated at any given snapshot.
Step 4: J-couplings
The primary discrepancy between the result of Figure 1(e) and the experimental measurement of Figure 1(a) is the presence of J-couplings associated with the CH2 and CH3 groups. See the J-couplings tutorial for a deeper explanation of the meaning of J-couplings and their simulation. The control.in file used for this purpose follows:
xc pbe
vdw_correction_hirshfeld
spin none
relativistic atomic_zora scalar
basis_threshold 0.0
magnetic_response j
+ ['NAO-J-5' species defaults for H, C, and O]
Given the relatively small size of the dimer, NAO-J-5 basis sets are possible here. For larger, more complicated molecules, NAO-J-4 basis sets will provide similar accuracy at substantially lower computational cost.
The J-couplings of each structure of the 10 selected from the AIMD ensemble were then computed. Averaging across these structures and across symmetry groups, the average J-coupling between the protons in the CH2 group and those in the CH3 group is computed to be 6.49 Hz. Under an experimental frequency of 89.56 MHz, this corresponds to a J-coupling of 0.0725 ppm. This J-coupling can be applied to the spectrum using multiplicity rules for the interaction between CH2 and CH3, leading to fourfold splitting of the former and threefold splitting of the latter peak in Figure 1(f). This final result simulates the experimental result of Figure 1(a) with relatively low error (<0.3 ppm). This tutorial illustrates how mechanistic hypotheses for the behavior of a substance can be tested by comparing to its experimental spectrum, though experience and significant familiarity with NMR beyond simple static DFT calculations is required. For advice on applying similar methodology to other materials, see the Further refinements section.
Further refinements
The above steps should be sufficient to produce well-behaved, accurate structures for a range of molecules. However, for larger molecules that are sufficiently complex, additional refinement may be necessary to produce good spectra. For many structures, groups of symmetry equivalent atoms can be averaged in a straightforward manner as described in Step (3). However, in some structures it is unclear what does or does not constitute such a symmetry-related group in a structure. For instance, consider a benzene ring where one proton has been removed to incorporate the ring into the larger molecule. Should all remaining protons be averaged equally into the same symmetry group? Does a symmetry group remain at all? There is no single answer for how a symmetry-related group will behave so such questions have to be explored on a molecule by molecule basis to generate the most accurate spectrum. Additionally, as was clear in the case of ethanol, including multiple molecules or an entire solvent environment to simulate bonding effects can be important to produce correct spectra.
In contrast to the ambiguity of symmetry averaging, with time-averaging, systematic improvement is possible. First, on the molecular dynamics simulation, there are three avenues of systematic improvement. First, larger and better converged basis sets will lead to more realistic molecular dynamics and better final spectra. Second, shorter time periods for each step will ensure each molecular motion is explored in fine detail. Finally, a longer overall molecular dynamics simulation will ensure that more molecular motions are fully captured, especially in molecules that tend to jump between different conformers during molecular dynamics (such as is expected to be the case in the association and dissociation of ethanol molecules here).
Second, on the geometry selection for time-averaging, there are two avenues of systematic improvement. Rather than random structure selection from the molecular dynamics ensemble as is done in (3), known modes of molecular motion can be determined and structures representing the full range of each motion can be selected as part of the eventual spectra. Second, increasing the number of structures included in the time-averaging improves the final spectra. In experimental NMR, there is effectively a "continuous" time-averaging where all structures present through the data collection time are averaged into the final result. As the number of geometries selected for time-averaging increases, the approximation of this continuum improves systematically.